Muitas vezes as pessoas perguntam como é que os astrônomos conseguem medir o tamanho de objetos no céu, por exemplo: como podemos saber o tamanho de um planeta ou mesmo da Lua e ainda mais, como saber o tamanho das crateras e outros acidentes sobre a superfície da Lua? Veremos aqui como procedimentos simples aliados a um pouco de matemática elementar nos permitem realizar medidas de objetos astronômicos. É sobre isso de que se trata este artigo.
Primeiramente vejamos como podemos conhecer o Diâmetro da Lua. Sabemos hoje, com boa precisão, que o diâmetro da Lua é em torno de 3474 km. Historicamente o primeiro astrônomo a determinar o diâmetro da Lua foi Aristarco de Samos na antiga Grécia. Mas aqui não abordaremos o método de Aristarco. Já no século XVII o grande físico Isaac Newton já inferira, usando a sua lei da Gravitação Universal, que a Lua deveria ter uma distância da Terra de cerca de 60 vezes o raio da própria Terra, o qual também já era conhecido com boa precisão nesta época.
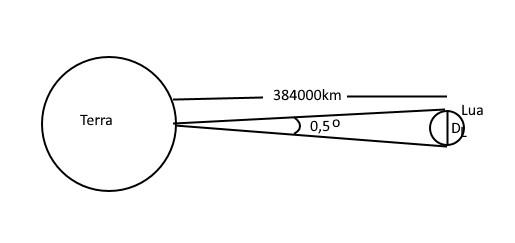
Figura 1: Esquema para a determinação do diâmetro da Lua.
Assim conhecendo o diâmetro angular da Lua (veja a figura 1), que é cerca de 0,5 grau (30 minutos de arco) e o raio da Terra que cerca de RT = 6400km pode-se deduzir o diâmetro DL da Lua pela expressão:
DL = dTL x tan (0,5o)
Sabendo que a distância da Terra à Lua dTL vale 60xRT, então: dTL = 60x6400km = 3,84×105 km. A qual é uma boa aproximação para a distância da Terra à Lua. Com uma calculadora obtemos tan(0,5o) = 8.72687×10-3 Assim: DL = 3,84×105 x 8.72687×10-3 = 3,4×103 km. A qual é uma aproximação razoável do diâmetro atualmente considerado. Usaremos neste experimento este valor aproximado para 3.5 x103km mais próximo do valor aceito atualmente.
Tendo em mãos o diâmetro da Lua, poderemos utilizá-lo como referência para a determinação de alguns grandes acidentes na superfície da Lua. Para isto precisaremos de uma imagem da Lua impressa na tela de um monitor de computador (ou em papel se você preferir), de uma régua milimetrada e um pouco de matemática básica. Você mesmo poderá obter a imagem da Lua com seu telescópio e celular. Veja isto no tópico sobre astrofotografia: Fotografando pelo método afocal. Devemos levar em consideração que este experimento é uma estimativa dos tamanhos dos acidentes lunares pois as medidas serão feitas sobre uma impressão plana de um objeto esférico e isso acarretará pequenos erros em nossas medidas que serão maiores quanto mais o objeto a ser medido esteja longe do centro do centro da esfera lunar projetada.
Suponhamos que desejamos medir o diâmetro da cratera Tycho. Para isto precisaremos de uma imagem que contenha a Lua de forma que seja possível medir seu diâmetro e outra fotografia tirada na mesma escala da primeira que contenha a cratera Tycho. No nosso caso uma única foto serviu para o nosso propósito. Vejamos o passo a passo:
- Com a imagem colocada sobre o monitor (ou folha de papel) meça o diâmetro da imagem da Lua em milímetros, veja a figura2.
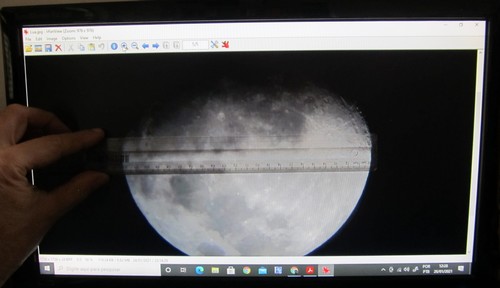
Figura 2: Medindo o diâmetro da imagem da Lua com uma régua milimetrada.
No nosso caso o diâmetro da Lua na escala medida foi dL = 221,0 mm.
- Agora mediremos com a fotografia, na mesma escala, o diâmetro da imagem da cratera Tycho. Veja a figura 3.

Figura 3: Medindo o diâmetro da cratera Tycho com a régua milimetrada.
O valor que assim obtivemos para o diâmetro de Tycho foi dac = 5,0mm.
3. agora utilizaremos a expressão de proporcionalidade:
Dac/dac = DL /dL
Onde:
Dac é o tamanho real do acidente,
dac é o tamanho do acidente medido na imagem,
DL é o diâmetro real da Lua,
dL é o diâmetro da imagem da Lua,
Assim poderemos escrever:
Dac/5,0 = 3,5X103/221,0
O que nos dá:
Dac = 79,2 km de diâmetro aproximadamente.
O tamanho real de Tycho é de 86,21 km, o que nos fornece um erro de aproximadamente 9%. Valores melhores podem ser obtidos quanto melhores forem os instrumentos e as medidas efetuadas. Levando em consideração a esfericidade da Lua, as aproximações dos valores utilizados e o caráter didático do experimento, considero este erro muito bom devido as condições e instrumentos utilizados. Este procedimento serve também para a medida de extensões de manchas solares.
Então, vamos medir o tamanho de acidentes da Lua?