
ADVERTÊNCIA:
ANTES DE FAZER ESTE EXPERIMENTO CERTIFIQUE-SE DE NÃO OLHAR DIRETAMENTE PARA O SOL. OLHAR DIRETAMENTE PARA O SOL PODERÁ CAUSAR DANOS IRREVERSÍVEIS A SUA VISÃO. ESTE EXPERIMENTO DEVERÁ SER REALIZADO DE FORMA QUE SEUS OLHOS NÃO SEJAM APONTADOS DE FORMA DIRETA PARA O SOL. NÃO ME RESPONSABILIZO POR NENHUM DANO CAUSADO AOS SEUS OLHOS OU SUA SAÚDE DE FORMA GERAL. CRIANÇAS NÃO DEVERÃO REALIZAR ESTE EXPERIMENTO A NÃO SER COM O ACOMPANHAMENTO DE UM ADULTO RESPONSÁVEL.
Este experimento tem por objetivo determinar o diâmetro do Sol usando um câmara escura de orifício com dados (atualizados) obtidos por métodos desenvolvidos pelos antigos astrônomos gregos. Aprender astronomia é também aprender seus métodos.
Dentre os ramos da Astronomia, temos a Astrometria, onde segundo a Wikipédia significa:
“Astrometria ou astronomia de posição é o ramo da Astronomia que lida com a medida precisa da posição das estrelas e de outros corpos celestes, assim como de suas distâncias e seus movimentos. “
Vários ramos da Astronomia, como a Astrofísica, dependem muito da Astrometria para determinar as características físicas de um astro. Para isto, muitas vezes, é preciso determinar as dimensões e/ou distância do objeto em estudo. Uma destas características poderia ser, por exemplo: a magnitude absoluta, a medida do brilho intrínseco de um objeto celeste. Para esta determinação é necessário saber a distância do objeto até nós. Assim determinar as distâncias e as dimensões dos astros são objetivos importantíssimos para a Astronomia.
Desde a época dos antigos gregos já eram conhecidos métodos para a determinação das distâncias da Terra ao Sol e da Terra à Lua e dos respectivos diâmetros desses astros (incluindo o da Terra). Hiparcus de Nicéia (190 a.C. – 120 a.C.) já havia determinado que a distância da Terra a Lua seria em torno de 30 vezes o diâmetro da Terra e Eratóstenes de Cirene (276 a. C. – 194 a.C.) já havia medido a circunferência da Terra em 250.000 estádios (40.000 km aproximadamente) o que nos fornece um diâmetro aproximado de 12.800 km para a Terra.
Aristarco de Samos (310 aC – 230 a.C.) utilizando-se de observações das fases da Lua e da geometria conseguiu avaliar uma distância entre a Terra e o Sol. Apesar de não ter determinado corretamente essa distância devido a algum erro cometido na determinação experimental do ângulo formado pela Lua, Sol e Terra , o qual foi avaliado em 3 graus e também no diâmetro angular do Sol, medido como 2 graus. Os valores obtidos por Aristarco foram muito diferentes dos aceitos atualmente, porém o método de Aristarco, com as devidas correções de tais medidas, fornece com boa precisão a distância da Terra ao Sol.
Para fazer essas determinações Aristarco se baseou nas seguintes hipóteses:
- A Lua é iluminada pelo Sol.
- A Lua possui órbita circular e no centro desta está a Terra.
- Nas fases quarto crescente e minguante a linha que divide o circulo da Lua nas partes brilhante e escura é paralela à linha que liga a Terra à Lua.
- No momento em que a Lua está nas fases quarto crescente ou quarto minguante o ângulo Lua, Sol, Terra vale 3 graus.
- Os Diâmetros angulares da Lua e do Sol valem 2 graus com relação à Terra.
- O diâmetro do cone de sombra da Terra é o dobro do diâmetro da Lua.
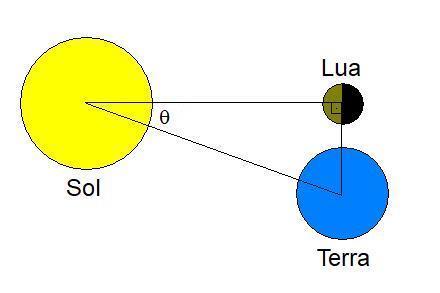
Figura 1. Esquema usado por Aristarco para as determinações das distâncias da Lua e do Sol à Terra.
Com os dados obtidos, Aristarco determinou que a distância Terra-Sol seria de 19 vezes o diâmetro da Terra, valor este aceito atualmente em torno de 380 vezes, e que o diâmetro do Sol seria de 6,7 vezes o diâmetro da Terra, 109 vezes em valores atuais. Hoje o valor medido para o ângulo Lua, Sol, Terra é de 0,15o . Serão utilizados os valores atualizados das medidas em nossos cálculos, mas ao invés de usarmos o diâmetro angular do Sol, atualizado em aproximadamente 0,5o, iremos utilizar uma câmara escura de orifício e a partir do diâmetro da imagem obtida calcularemos o diâmetro do Sol. Pode-se obter a distância da Terra ao Sol pelo método de Aristarco utilizando modelo da figura 1.
Assim temos que: o ângulo θ formado pela Terra, Sol e Lua vale 0,15o , e que o seno do ângulo θ será a razão da distância da Terra à Lua (D1) pela distância da Terra ao Sol (D2). Assim sen 0,15 = D1 / D2. Consultando uma tábua trigonométrica ou uma calculadora científica podemos obter o seno de 0,15o, que vale aproximadamente 0,00262. Então podemos escrever que: 0,00262 = = D1 / D2 , onde então, D2 = D1 /0,00262 = 382 D1. Como D1 = 30 x Diâmetro da Terra = 30 x 1,28 x 104 km = 3,84 x 105 km. E assim D2 = 382 x 3,84 x 105 km = 1,47 x 108 km. Valor este que apresenta um erro de aproximadamente 10% com relação ao atual valor da distância média do Sol até a Terra que vale 1,496 x 108 km. Deste modo adotaremos o valor de 1,47 x 108 km como valor para a distância da Terra ao Sol em nossos cálculos. Isso não atrapalha os resultados, pois em geral o Sol estará numa distância diferente de 1,496 x 108 km devido ao formato da órbita da Terra ser uma elipse. É importante observar que as operações realizadas como os valores acima foram feitas levando em consideração apenas 3 algarismos significativos o que é mais que o suficiente para o propósito deste experimento.
O objetivo principal desta atividade experimental é determinarmos com precisão relativamente boa o diâmetro do Sol. Para tal finalidade será utilizado um antigo instrumento óptico: uma câmara escura de orifício, como a representada na figura 2.
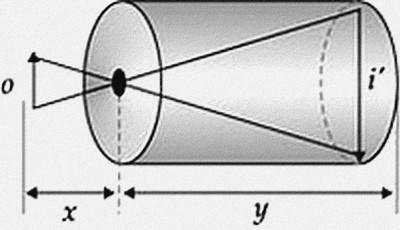
Figura 2: Câmara escura de orifício. Aqui vale a relação: i/o = y/x.
Onde: o, é o tamanho do objeto e será o diâmetro do Sol a ser calculado; i, é o tamanho da imagem projetada do objeto; x, é a distância do objeto a câmara, será a distância da Terra ao Sol e y, é o comprimento da câmara.
Lá na Física, no assunto de óptica geométrica, estudamos que a relação i/o = y/x é válida para a câmara escura. Usaremos esta expressão para calcular o diâmetro do Sol. Mas para isso precisaremos obter o valor de i (tamanho da imagem) numa câmara escura.
Construção da Câmara Escura
Material utilizado:
- uma cartolina tipo guache de cor preta;
- uma folha de papel vegetal ou no caso da falta deste pode ser o chamex.
- Tesoura;
- Cola para papel;
- Lápis.
- três elásticos de dinheiro.
- Agulha ou prego fino.
- Régua milimetrada.
Procedimento:
1. Corte a cartolina pela metade e monte um cilindro de diâmetro entre 6 e 8 centímetros de forma que o comprimento do tubo seja o maior comprimento da cartolina. Certifique-se de que o tubo está bem colado e sem brechas. Para isso cole a cartolina e a prenda com os elásticos de dinheiro até que a cola fique completamente seca. A parte preta da cartolina deverá ficar na parte interna do cilindro.

Figura 3: Tubo de cartolina colando.
2. Com o lápis sobre a outra metade da cartolina, marque um círculo usando como contorno uma das bases do cilindro. Corte um círculo ligeiramente maior que o diâmetro do cilindro e o cole fechando a base correspondente. Com uma agulha ou prego fino faça um furo bem no centro do círculo. Esta sera a face que será apontada para o Sol. Veja na figura 4 como isto ficou montado e note que a parte preta da tampa ficou para dentro do tubo.

Figura 4: Tampa de umas das bases do cilindro. Neste caso essa sera a face (frente do tubo) que deverá ser apontada para o Sol.
3. Faça novamente o que foi feito no item 2 só que com o papel vegetal (ou chamex). Esta face não deverá ser furada. Ela será a tela na qual será projetada a imagem do disco solar.

Figura 5: Com o papel vegetal (ou chamex) será construída a tampa (fundo do tubo) que será a tela de projeção da imagem do disco solar.
Meça, com uma régua milimetrada, o comprimento (y) da câmera escura e anote o valor.
Pronto a câmara escura de orifício está montada e pronta para uso.
Uso do dispositivo
Aqui mais uma vez quero advertir que olhar diretamente para o Sol, em quaisquer circunstâncias, poderá causar danos irreversíveis a visão, portanto todo o cuidado com seus olhos é pouco. Ao apontar o dispositivo procure algo como um muro ou uma mureta para apoiar o dispositivo e ficar protegido da ação direta dos raios solares. Evite fazer este experimento entre as 10 hs e as 14 hs, horários em que o Sol está muito intenso e no qual há pouca proteção de sombras.
Apoie a câmara escura sobre uma mureta de forma que você fique na parte da sombra protegido dos raios solares e aponte a face com o furo na direção do Sol. Vá procurando a imagem do Sol, sem olhar diretamente para ele, girando e movendo a câmara para cima e para baixo para um lado e para o outro até que uma pequena imagem do disco solar apareça na tela de projeção da câmara. Apoie uma régua nesta face e com ela tente medir o diâmetro da imagem projetada. Se possível faça várias medidas e use o valor médio delas nos seus cálculos. Quanto mais medidas forem feitas mais será preciso o resultado.

Figura 6: Com a câmara apoiada e com o observador protegido do Sol pode-se efetuar a medida da imagem solar com uma régua. Note na parte superior da tela de projeção uma pequena imagem do disco solar.
Qual valor você encontrou para o diâmetro da imagem Solar?
Faça as contas e compare com o valor aceito atualmente (1,40 x 106 km).
Qual o erro em porcentagem com relação ao valor aceito atualmente e o medido por você?
Para título de exemplo, a câmera escura montada aqui tem 485 mm de comprimento e o diâmetro da imagem do Sol medido por esta câmara foi de 4,5 mm, assim:
i = 4,5 mm;
x = 1,47 x 108 km;
y = 485 mm;
o, é o que queremos calcular.
Usando a expressão da câmara escura descrita anteriormente temos:
4,5/o = 485/1,47 x 108 km
onde obtemos:
o = 1,36 x 106 km com um erro de aproximadamente 3%. O qual é um excelente resultado para o tipo de material utilizado no experimento.